2. Conduction :
Conduction heat transfer is the transfer of heat by means of molecular excitement within a material without bulk motion of the matter. Conduction heat transfer in gases and liquids is due to the collisions and diffusion of the molecules during their random motion. On the other hand, heat transfer in solids is due to the combination of lattice vibrations of the molecules and the energy transport by free electrons.
2.1 Fourier Law :
The basic relation of heat flow by conduction is the proportionality between the rate of heat flow across an isothermal surface and the temperature gradient at the surface. It is called Fourier’s law.
Conduction under the condition of constant temperature distribution is called steady state conduction. The temperature is function of position/distance only and rate of heat flow at any one point is constant. The equation is given as
\( \frac{dq}{dA} = -\frac{k \partial T}{\partial x} \)Where, q is rate of heat flow across surface in direction normal to surface
- A is area of isothermal surface
- k is thermal conductivity
- T is temperature
- x is distance measured normally to surface
Thermal Conductivity: The proportionality constant k is a physical property of the substance called the thermal conductivity. It is like Newtonian viscosity mu is one of the so-called transport properties of the material.
Units of k are (W/m-C) or (Btu/ft2-hr-(F/ft)) or (Btu/hr-ft-F)
Fourier's law states that k is independent of the temperature gradient but not necessarily of temperature itself. Experiment does confirm the independence of k for a wide range of temperature gradients, except for porous solids, where radiation between particles, which does not follow a linear temperature law, becomes an important part of the total heat flow. On the other hand, k is a function of temperature, but not a strong one. For small ranges of temperature, k may be considered constant. For larger temperature ranges, the thermal conductivity can usually be approximated by an equation of the form
k= a +bTWhere a and b are empirical constants.
| Thermal Conductivity | Btu/ft-h-°F | W/m-°C |
|---|---|---|
| Metal (stainless steel) | 10 | 17 |
| Metal (Silver) | 240 | 416 |
| Glass and nonporous minerals | 0.2 to 2 | 0.35 to 3.5 |
| Water | 0.3 to 0.4 | 0.5 to 0.7 |
| Gases Air (at 0 C) | 0.014 | 0.024 |
The thermal conductivity of gases is almost independent of pressure but increases with temperature due to molecular velocity increase. Solids that have low k values are used as heat insulators to reduce the heat loss. Porous insulating materials such as polystyrene foam work by clogging up air and preventing convection. Their k-values are roughly equal to air itself.
2.2 Steady State Conduction :
Consider a flat slab as shown in Figure 1.
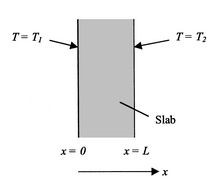
Assumptions:
- k is independent of temperature
- The area of the wall is very large in comparison with its thickness, so that heat losses from the edges are negligible.
- The external surfaces are at right angles to the plane of the illustration, and both are isothermal surfaces.
- The direction of heat flow is perpendicular to the wall.
- Steady state (neither accumulation nor depletion of heat within the slab)
If x is the distance from the hot side, then
\(q/A = -k \, dT/dx\)or
\(dT = -\frac{q}{kA} dx\)Direct integration gives
\(q/A = -k \frac{T_1 - T_2}{x_2 - x_1}\) = \(\frac{\Delta T}{L}\)Where, \(x_2 - x_1\) = L = thickness of slab
\(T_1 - T_2 = \Delta T\) = temperature drop across slab
When the thermal conductivity k varies linearly with temperature, k can be found either by using the arithmetic average of the individual values of k for the two surface temperatures, T, and T2, or by calculating the arithmetic average of the temperatures and using the value of k at that temperature.
\(q/A = \frac{\Delta T}{R}\)Where, R is the thermal resistance of the solid between points 1 and 2 (R=L/k).
Heat rate (q) is the ratio of a driving force ∆T to a resistance (R). The reciprocal of a resistance is called a conductance, which for heat conduction is k/L. Both resistance and the conductance depend upon the dimensions of the solid as well as on the conductivity k.
2.3 Compound Resistances in Series :
Consider a flat wall constructed of a series of layers as shown in following Figure 2.
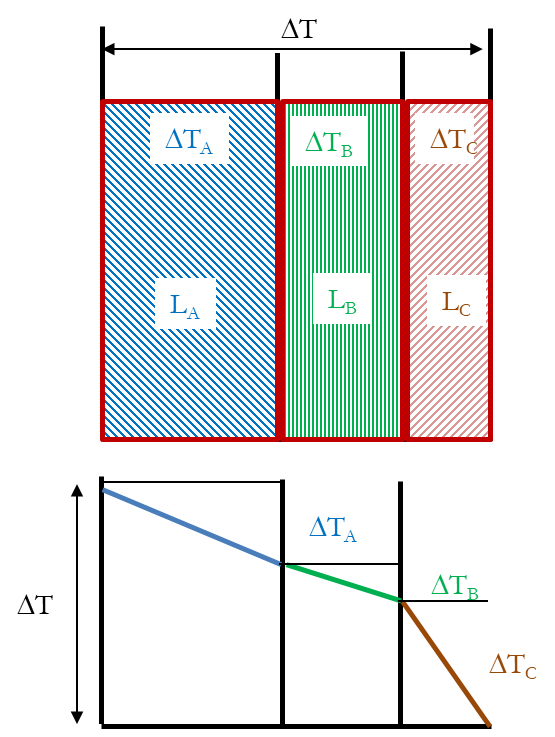
Figure 2: Thermal Resistances in Series
- Thicknesses of the layers be \(L_A\) \(L_B\) and \(L_C\)
- Average conductivities of the materials of which the layers are made be \(k_A\) \(k_B\) and \(k_C\)
- \(\Delta T_A\) \(\Delta T_B\) and \(\Delta T_C\) be the temperature drops across layers A, B, and C
- Area of the wall is “A”
Assume that the layers are in excellent thermal contact, so that no temperature difference exists the layers are in excellent thermal contact, so that no temperature difference exists across the interfaces between the layers.
\(\Delta T\) is the total temperature drop across the entire wall is given by
\(\Delta T = \Delta T_A - \Delta T_B + \Delta T_C\)Using steady equation of heat rate, equation can be written for each layer
\(\Delta T_A = \frac{q_A L_A}{k_A A}\) \(\Delta T_B = \frac{q_B L_B}{k_B A}\) \(\Delta T_C = \frac{q_C L_C}{k_C A}\)Adding above equations:
\(\Delta T_A + \Delta T_B + \Delta T_C = \frac{q_A L_A}{k_A A} + \frac{q_B L_B}{k_B A} + \frac{q_C L_C}{k_C A} = \Delta T\)In steady heat flow, all the heat that passes through the first resistance must pass through the second and in turn pass through the third, \(q_A\) \(q_B\) and \(q_C\) are equal and all can be denoted by q. Using this fact and solving for q/A gives
Equation
\(\frac{q}{A} = \frac{\Delta T}{L_A/k_A + L_B/k_B + L_C/k_C} = \frac{\Delta T}{R_A + R_B + R_C} = \frac{\Delta T}{R}\)Where \(R_A\),\(R_B\),\(R_C\) = Resistance of individual layers
R= Overall resistanc
- Heat flow through a series of layers the overall thermal resistance equals the sum of the
individual resistances.
The rate of flow of heat through several resistances in series clearly is analogous to the current flowing through several electric resistances in series.
The ratio of total temperature drop to total resistance is equal to ratio of individual temperature drop in layer to individual layer resistance.
\(\frac{\Delta T}{R} = \frac{\Delta T_A}{R_A} = \frac{\Delta T_B}{R_B} = \frac{\Delta T_C}{R_C}\)Depending on the thickness and thermal conductivity of the layer, the temperature drop in that layer may be a large or small fraction of the total temperature drop. A thin layer of low
conductivity may cause a much larger temperature drop and a steeper thermal gradient than a thick layer of high conductivity as shown in Figure 2.
2.4 Heat flow through a cylinder :
Consider the hollow cylinder shown in Figure 3. The inside radius of the cylinder is\(r_i\), the outside radius is \(r_0\) and the length of the cylinder is L.
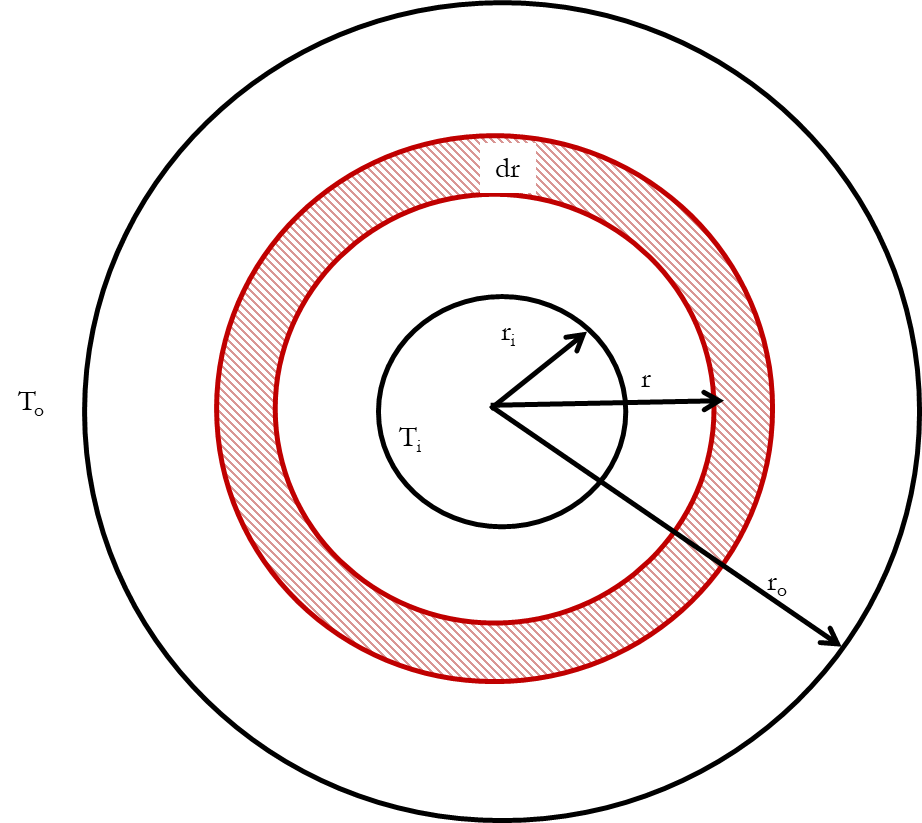
Figure 3: Heat Flow through thick wall cylinder
The thermal conductivity of the material of which the cylinder is made is k. The temperature of the outside surface is \(T_0\), and that of the inside surface is \(T_i\). It is desired to calculate the rate of heat flow outward for this case.
Consider a very thin cylinder of radius “r”. The thickness of the wall of this cylinder is “dr”. If “dr” is small enough with respect to “r” for the lines of heat flow to be considered parallel.
\(q = -k \frac{dT}{dr} 2\pi r L\)Since the area perpendicular to the heat flow is equal to 2πrL.
Integrating equation
\(\int_{r_i}^{r_o} \frac{dr}{r} = \frac{2\pi L k}{q} \int_{T_o}^{T_i} dT\) \(q = \frac{k (2\pi L) (T_i - T_o)}{\ln \frac{r_o}{r_i}}\)Equation can be used to calculate the flow of heat through a thick-walled cylinder. It can be put in a more convenient form by expressing the rate of flow of heat as
\(q = \frac{k A_L (T_i - T_o)}{r_o - r_i}\)This is of the same general form as for heat flow through a flat wall with the exception of\(A_L\), which must be so chosen that the equation is correct.
\(A_L = \frac{2\pi L (r_o - r_i)}{\ln\left(\frac{r_o}{r_i}\right)}\)\(A_L\) is the area of a cylinder of length L and radius \(r_L\) where
\(r_L = \frac{r_o - r_i}{\ln\left(\frac{r_o}{r_i}\right)}\)\(r_L\) is called the logarithmic mean radius. It is the radius that, when applied to the integrated equation for a flat wall, will give the correct rate of heat flow through a thick-walled cylinder.
The logarithmic mean is less convenient than the arithmetic mean, and the latter can be used without appreciable error for thin-walled tubes, where \(\left(\frac{r_o}{r_i}\right)\) is nearly 1.